How is gradient a one form?
One form is a tensor or a rule that takes one vector as an
argument and returns a real number. Simply it is a mapping from vector to real
number. Gradient is a commonly known one form. To understand how a gradient is
a one form, consider the following diagram.
Suppose 𝜙(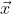 ) is a scalar field defined at every
event
) is a scalar field defined at every
event 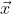 . Its value changes from event to event. The scalar field is a function
of coordinates of events.
. Its value changes from event to event. The scalar field is a function
of coordinates of events.
![\phi (\vec{x}) = \phi[t, x , y , z ]](https://latex.codecogs.com/gif.latex?\phi&space;(\vec{x})&space;=&space;\phi[t,&space;x&space;,&space;y&space;,&space;z&space;])
The curve shown in
the figure is the world line of a particle. At every point of that curve the
scalar field 𝜙(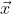 ) gives some real number value. t is the time for a particular
event measured by the observer 𝓞. Now consider the proper time 𝜏 which is
measured by the particle itself in its frame. If we label all the events by the
proper time 𝜏, you can treat the coordinates of the events on its world line
as scalar functions of 𝜏.
) gives some real number value. t is the time for a particular
event measured by the observer 𝓞. Now consider the proper time 𝜏 which is
measured by the particle itself in its frame. If we label all the events by the
proper time 𝜏, you can treat the coordinates of the events on its world line
as scalar functions of 𝜏.
![[ t = t(\tau ), x = x(\tau), y = y(\tau), z = z(\tau)]](https://latex.codecogs.com/gif.latex?[&space;t&space;=&space;t(\tau&space;),&space;x&space;=&space;x(\tau),&space;y&space;=&space;y(\tau),&space;z&space;=&space;z(\tau)])
For every value of 𝜏, there are real number values of those coordinates. As the coordinates themselves are functions of the proper time 𝜏, 𝜙 is also a function of proper time 𝜏.
![\phi (\tau) = \phi[ t = t(\tau ), x = x(\tau), y = y(\tau), z = z(\tau)]](https://latex.codecogs.com/gif.latex?\phi&space;(\tau)&space;=&space;\phi[&space;t&space;=&space;t(\tau&space;),&space;x&space;=&space;x(\tau),&space;y&space;=&space;y(\tau),&space;z&space;=&space;z(\tau)])
For every value of 𝜏, there are real number values of those coordinates. As the coordinates themselves are functions of the proper time 𝜏, 𝜙 is also a function of proper time 𝜏.
Now if we want to determine the rate of change of the scalar
field 𝜙 along the curve, we have to find the value of d𝜙/d𝜏.
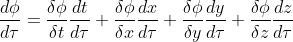
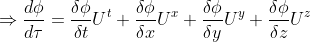
It is clear from the last equation that from the vector  we
get the number d𝜙/d𝜏 which represents the rate of change of 𝜙 on a curve on
which
we
get the number d𝜙/d𝜏 which represents the rate of change of 𝜙 on a curve on
which  is tangent. As you can see the number d𝜙/d𝜏 is a linear function of
is tangent. As you can see the number d𝜙/d𝜏 is a linear function of  , so we have defined a one-form. The one form has components
(𝛿𝜙/𝛿t,𝛿𝜙/𝛿x,𝛿𝜙/𝛿y,𝛿𝜙/𝛿z). This one form is called the gradient of 𝜙 denoted by d̃𝜙:
, so we have defined a one-form. The one form has components
(𝛿𝜙/𝛿t,𝛿𝜙/𝛿x,𝛿𝜙/𝛿y,𝛿𝜙/𝛿z). This one form is called the gradient of 𝜙 denoted by d̃𝜙:
This gradient satisfies all the axioms of one form. Note
that the rate of change of the scalar field 𝜙 is a scalar product of d𝜙/d𝑥⃗ and d𝑥⃗/d𝜏. So,
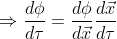
(from partial derivative we can say that).The scalar product is a rule that takes two vectors and gives a real number. If only one vector is passed to the scalar product rule then it still lacks one vector. This can be treated as a one form rule that takes a vector and makes the scalar product between the two vectors. For an example, suppose a rule g̃( ,
, ) =
) =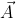 .
.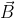 . If we pass only one vector g̃(
. If we pass only one vector g̃(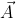 , ) lacks one. So, g̃(
, ) lacks one. So, g̃(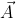 , )can
be treated as an another rule Ã( ) which is a one form and takes only one
vector and is defined by Ã(
, )can
be treated as an another rule Ã( ) which is a one form and takes only one
vector and is defined by Ã(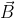 ) =
) = 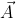 .
. . Similarly, d̃𝜙 is a one form that takes a
vector as an argument and gives a real value which is the scalar product of
d𝜙/d𝑥⃗(called the gradient vector) and the vector. To find the rate of change
of 𝜙 along the curve we have to pass the tangent four velocity vector
. Similarly, d̃𝜙 is a one form that takes a
vector as an argument and gives a real value which is the scalar product of
d𝜙/d𝑥⃗(called the gradient vector) and the vector. To find the rate of change
of 𝜙 along the curve we have to pass the tangent four velocity vector  as an
argument to the gradient d̃𝜙. It is very much important for you to understand
that d̃𝜙 itself is not the change of the scalar field 𝜙 along the curve on
which
as an
argument to the gradient d̃𝜙. It is very much important for you to understand
that d̃𝜙 itself is not the change of the scalar field 𝜙 along the curve on
which  is tangent. It is just a rule that takes the vector
is tangent. It is just a rule that takes the vector  and gives a real
number which is the rate of change of 𝜙 along the curve. So, you can see that
the gradient is actually a one-form.
and gives a real
number which is the rate of change of 𝜙 along the curve. So, you can see that
the gradient is actually a one-form.
(from partial derivative we can say that).The scalar product is a rule that takes two vectors and gives a real number. If only one vector is passed to the scalar product rule then it still lacks one vector. This can be treated as a one form rule that takes a vector and makes the scalar product between the two vectors. For an example, suppose a rule g̃(

Comments
Post a Comment
If you have any doubt please comment and let me know