What is one form?

One form is a tensor. Or simply one form is a rule that takes one vector as argument and gives a real number and is linear in its vector argument. One form is just a mapping from vector to real number i.e. it is a function of a vector that gives a real number. One form is denoted by p̃() (it is almost the same way we denote a normal function just with a '  ̃' symbol) where is a vector. Note that p̃() itself is not the one form, it is the value of the one form. p̃ itself is not the number p̃(), it is the rule that associates the real number with that vector . So, p̃() gives a real number. But we can define another one form q̃() so that

g̃ = p̃ + q̃

s̃ = 𝛼p̃

Which is equivalent to

g̃() = p̃() +q̃()

and s̃() = 𝛼p̃()

Note that p̃(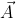) and q̃(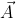) are actually real numbers, So, you can define any one-form on that particular vector 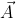to get those real numbers. Remember, like the last equation, any one-form multiplied with a constant real number (here 𝛼) itself is another one-form (it makes sense as it is also a rule). For example, if g̃(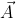) = 2 then we can define another one-form h̃(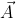) = 6 = 3 × 2 = 3 × g̃(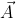). One more thing, the one form takes a vector, not the components of that vector. As we know that the components of a vector depends upon the frame but the vector itself doesn’t. So, the number p̃(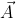) does not depend on the frame.
The one form is linear in its argument means that it satisfies the following conditions.

and,

With these rules the set of all one-forms satisfy the axioms of a vector space. This vector space is called “Dual vector space” to distinguish it from the “vector space”.

Components of a one-form:

Components of a particular one-form are the values of that one-form when the basis vectors are passed to it. Here, we are dealing with four dimensional spacetime. So, there are four basis vectors . Hence, the components of that one-form are as follows:

 where 𝛼 belongs to the set {0,1,2,3}(as we are dealing with 4 dimensional spacetime, so there are four basis vectors, each one denoted by ). We denote components of a one form, by convention, with a single lower index. For a particular component of  the one form p̃, 𝛼 can take a value from the set. So, as there are four basis vectors, there are four components of a one-form. Remember, any component with a upper index denotes the component of a vector (). Don't be confused here. Any four components (2,3,5,0) itself does not define any thing unless specified whether these are components of a vector or a one-form. We know that any four dimensional vector can be determined by its components and by the basis vectors of that frame.  

Now, consider this,

Here we have used Einstein summation convention where

As the one form p̃ is linear in its argument, so we can write,

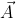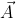So, you can see that the real number p̃() is found to be the sum . This is called of   and p̃. Remember, as the p̃(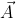) is frame independent, so its value should also be frame invariant. So,   altogether is frame invariant though both the components of the vector and the one-form depend on the frame. The total value, however, is frame invariant. Gradient is a common example of one-form. If you want to know a gradient  is a one-form click here.