Basis four vectors in spacetime:

In three dimensional spatial coordinate system, we use unit vectors along the three standard directions which are 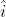in x direction, 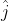in y direction and 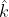in z direction and are defined by –

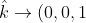 Defining unit vectors helps us to determine a particular vector just by knowing its components –

Where x , y and z are the components of vector A.

Similarly, in four dimensional spacetime, we take help of the basis four vectors. They are used in the same way as the unit vectors in three dimensional space are used. These are very similar to the unit vectors in three dimensional Euclidean space and are defined by –

Note that we have defined the basis vectors of the frame O. These basis vectors will be different in different frame. For an observer , the basis four vectors are –

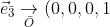If you relate between the corresponding basis vectors of O and , you will see that there are no difference between them. But think carefully, though their components are same but they themselves are not the same vectors. Remember that we are defining the basis vectors of O and  in different frames. So, the time axis of O and the time axis of are not the same vector. That means that in ’s frame is defined by –

But the same vector becomes –

in O’s frame. Here, v is the speed of  relative to O and   we have used Lorentz Transformation to transform the components of   measured by  into the components measured by O( Lorentz Transformation is the transformation of coordinates of a particular event with the change of frames). So, you can see that basis vectors depend on the frames. Every frame has its own set of four basis vectors. Their components are same but the vectors themselves are not the same.

Suppose a vector A has the following components –

Then it can be defined by –

 or in short –

Here we have used the Einstein summation convention which states that can be written as to make it simpler to read and understand( for a newcomer to the theory of relativity, using summation signs might seem to be easier to use but in more complex calculations, writing a series of summation signs is not a good deal).  

The same vector can be defined by –

where the components of the vector and the basis vectors are measured in  frame. This implies that —