Four vectors in spacetime
A vector is nothing but a straight line with a specific
direction. Any event in spacetime can be represented by a four vector. If you
know what spacetime is, you will agree that the “spacetime” is made of 4 dimensions
– three spatial dimensions and the time dimension(If you don’t have any idea
about “spacetime” then you can go through our article on spacetime – “What is
spacetime?”). So, a vector in spacetime has four coordinates and so its name. As
like the vectors in three dimensional Euclidean space, a four vector is something
whose components transform as do the coordinates under a coordinate
transformation. It means that if you change the coordinate system then the
components of the four vector measured by you will be different from the
previous measurements. But the vector itself does not change. It remains the
same i.e. its magnitude and direction does not change. A four vector is the displacement
vector which points from one point to another and its components are equal to
the coordinate differences. If the coordinate system is changed then the
coordinates of the two points will change and so the components of the vector. Four
vector is denoted by the following notation
An arrow over  says that
says that  is a vector and the arrow
after
is a vector and the arrow
after  says that “it has components”. O below the second arrow says that the
components after the second arrow are measured “in the O frame”(It is important
to know in which frame you are doing the measurements because the coordinates
change as the coordinate system changes). The coordinates of a four vector is
written in the same order as shown in (1). Don’t forget that the vector
says that “it has components”. O below the second arrow says that the
components after the second arrow are measured “in the O frame”(It is important
to know in which frame you are doing the measurements because the coordinates
change as the coordinate system changes). The coordinates of a four vector is
written in the same order as shown in (1). Don’t forget that the vector  is between
the two events so changing the coordinate system will not affect the vector(
particularly the magnitude and the direction as I said earlier). The notation
(1) can also be written like the following
is between
the two events so changing the coordinate system will not affect the vector(
particularly the magnitude and the direction as I said earlier). The notation
(1) can also be written like the following
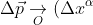)
Where 𝛼 can take values from the set {0,1,2,3}. It is
the shorthand for the notation (1).  is equivalent to
is equivalent to ) . If the observer is changed(i.e. the coordinate system is changed) then
the above notation can be written as –
. If the observer is changed(i.e. the coordinate system is changed) then
the above notation can be written as –
)
The bar over O and 𝛼 says that the components of the vector are measured in frame. Remember that the vector
frame. Remember that the vector  itself does
not change, it is the same vector and that’s why it does not need any bar over
it. Note that every coordinate system in spacetime (not only in spacetime but
also in two dimensional and three dimensional spaces) is somehow related with each
other. There are always some equations with which you can relate the two
different systems or frames. In four dimensional spacetime the frames are
related by their relative speed with each other. We can determine the relation
between the two frames using the Lorentz transformation rule.
itself does
not change, it is the same vector and that’s why it does not need any bar over
it. Note that every coordinate system in spacetime (not only in spacetime but
also in two dimensional and three dimensional spaces) is somehow related with each
other. There are always some equations with which you can relate the two
different systems or frames. In four dimensional spacetime the frames are
related by their relative speed with each other. We can determine the relation
between the two frames using the Lorentz transformation rule.
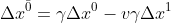

which can be written as


where and similarly for other components in the frame
and similarly for other components in the frame  . Note that we have used Einstein summation notation where
. Note that we have used Einstein summation notation where
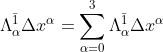
The bar over O and 𝛼 says that the components of the vector are measured in
which can be written as
where
A four vector multiplied with a constant number is itself a
new vector.
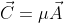
The magnitude of a four vector is equal to the interval between the two events.
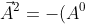^{2}&space;+&space;(A^{1})^{2}&space;+&space;(A^{2})^{2}&space;+&space;(A^{3})^{2})
The magnitude of a four vector is equal to the interval between the two events.
Comments
Post a Comment
If you have any doubt please comment and let me know