Velocity composition law in relativity
Velocity is a vector which has a direction and a magnitude.
We know that a resultant vector of two or more vectors can be determined by the
vector triangle law. Say for example, you are at rest in a station platform.
Your friend (say, his name is John) is in the train moving away from you with a
speed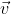 
. Now, suppose John has a ball and he throws the ball in the direction
of the motion of the train. The ball has a speed 
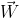relative to John. Now what
is the speed of the ball in your frame (i.e. with what speed is the ball moving
away from you?)? All you need to do is to ad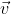d and 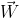(vector triangle law) and
the result is the answer to the above question. But suppose John has a light
source instead of a ball. When the light source emits light in the direction of
motion of the train, John measures the speed of light beam to be about
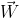(i.e. the magnitude of is now 
). If the train is moving at
the same speed 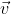relative to you then how would you calculate the speed of that
light beam? Can you just ad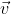d and 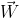? Well, in that case, you will find that
the light beam is moving faster than the speed of light which is allowed (we
know that nothing even the light itself can’t move faster than the speed c
where c has a value ). What is the answer then? The answer is c i.e.
. It means that you and John both will measure the same speed of light
(We know that the speed of light in vacuum is independent of observer’ motion. Every
observer will measure the same speed of light). So, you can see that the vector
triangle law does not help us when we are dealing with velocities comparable to
the speed of light. Can’t we define a way to handle all the cases. Yes we can.
We use Lorentz transformation law to define it. Consider the first example.
John is moving with speed 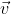relative to you and the ball has a speed 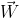relative
to John. John's world line is 
and your world line is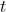 
. Velocity of the ball in John's frame is 
whereas in your frame the velocity of the ball is 
. John is moving with velocity 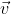relative to you. So, from Lorentz Transformation, we get,
/(\sqrt{1-v^2}) "\Delta x = (\Delta \bar{x}+ v\Delta \bar{t})/(\sqrt{1-v^2})")
and,
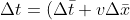/(\sqrt{1-v^2}) "\Delta t = (\Delta \bar{t}+ v\Delta \bar{x})/(\sqrt{1-v^2})")
and,
Now,
Note that here I have used the special measurement system where the speed of light is measured in meter and has a value exactly 1 (if you are wondering how it is possible, kindly go through our article "can the speed of light be exactly 1?"). You can see that the value of
which we experience in our daily life.
Comments
Post a Comment
If you have any doubt please comment and let me know