What is time dilation?
Time dilation is one of the most important results of
“Special theory of relativity”. In fact, it is the weirdest result of “Special
theory of relativity” which we never experience in our daily life. But how
weird and impossible it seems to be, it is verified in all the experiments. All
the experiments give the same result. Even it is experienced all the time in
nuclear reactions. So, let us understand “time dilation” in the simplest way,
with the spacetime diagrams. Here again we will assume the speed of light to be
exactly 1. If you are wondering how the speed of light is exactly 1 when its
value is ( ), go through the article “can the speed of light be exactly 1?”. So time and all the spatial
coordinates are measured in meters. Now consider the following diagram.
), go through the article “can the speed of light be exactly 1?”. So time and all the spatial
coordinates are measured in meters. Now consider the following diagram.
Suppose 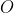 and
and  are two observers.
are two observers.  moves with
uniform velocity v(which is assumed to be near the speed of light) with respect
to the observer
moves with
uniform velocity v(which is assumed to be near the speed of light) with respect
to the observer 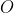 . The world line of
. The world line of 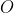 is the t axis(which means that
is the t axis(which means that 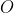 is rest
in his frame as he does not move in his frame though time is passing) and world
line of
is rest
in his frame as he does not move in his frame though time is passing) and world
line of  is
is  axis i.e.
axis i.e.  moves along the
moves along the  axis in the
spacetime diagram. Note that
axis in the
spacetime diagram. Note that  moves along the
moves along the  axis in the both frame
but the fact is that
axis in the both frame
but the fact is that  is at rest in
is at rest in  frame but is in motion in
frame but is in motion in 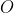 frame.
frame.
Here you can see that
the coordinate systems of the two observers are different which means that the
coordinates of events measured by 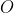 and
and  are different. They will measure
different time coordinate for the same event. Different observers calculate
different readings for the same event. For example, in two dimensional coordinate
system, different coordinate systems measure different positions(i.e. different
values of x and y coordinates) of the same point( see the figure below).
are different. They will measure
different time coordinate for the same event. Different observers calculate
different readings for the same event. For example, in two dimensional coordinate
system, different coordinate systems measure different positions(i.e. different
values of x and y coordinates) of the same point( see the figure below).
The same thing happens in 4 dimensional spacetime. Different
observers measure different coordinate values(including the time coordinate)
for the same event. Now consider the following diagram –
To understand time dilation, you should have a basic
knowledge of what interval in spacetime is. Consider the two dimensional
coordinate system(fig 2). Different systems measure different coordinate values
but notice one thing that the distance between the two points does not change.
It is fixed and does not depend on coordinate system. Similarly for the three dimensional
systems, different coordinate systems measure different values of the
coordinates but the distance between the two points does not change. The same
is applicable in four dimensional spacetime. The distance between the two
events does not depend on the coordinate system. This four dimensional distance
is called the “interval”. Interval is defined by the following equation –
^{2}&space;=&space;-(\Delta&space;t)^{2}&space;+(\Delta&space;x)^{2}+(\Delta&space;y)^{2}+(\Delta&space;z)^{2})
Suppose,  and
and 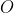 both have clocks which are set to zero
at point X and then started. Now, consider the point A at which
both have clocks which are set to zero
at point X and then started. Now, consider the point A at which  ’s clock
measure 1m(Note that time is measured in meter). Will the observer
’s clock
measure 1m(Note that time is measured in meter). Will the observer 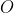 also
measure the same time? No! Say,
also
measure the same time? No! Say, 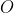 measures t time at event A. As we know, the
interval between two events is observer independent. Then the interval between
X and A is –
measures t time at event A. As we know, the
interval between two events is observer independent. Then the interval between
X and A is –
^{2}&space;=&space;-(\Delta&space;t)^{2}&space;+(\Delta&space;x)^{2}+(\Delta&space;y)^{2}+(\Delta&space;z)^{2})
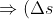^{2}&space;=&space;-(\Delta&space;\bar{t})^{2}&space;+(\Delta&space;\bar{x})^{2}+(\Delta&space;\bar{y})^{2}+(\Delta&space;\bar{z})^{2})
Now, is the time measured by
is the time measured by  and all the other coordinates are zero(as
and all the other coordinates are zero(as  is at rest in his frame). So, the second equation becomes,
is at rest in his frame). So, the second equation becomes,
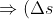^{2}&space;=&space;-1)
Now,
Now,
So, the calculations and the diagram suggest that the value of the time measured by the observer
You can see that



Comments
Post a Comment
If you have any doubt please comment and let me know